WebQuest Matemáticas Álgebra Ecuaciones Lineles, De Segundo Grado, Y De Tercer Grado
Ecuaciones Lineles, De Segundo Grado, Y De Tercer Grado
Publicado el 03 Abril de 2011
Autor: Saul E. Cadena Benitez
Introducción
ECUACIONES DE PRIMER GRADO
Una ecuación es una igualdad que sólo se verifica para unos valores concretos una variable, generalmente llamada x.
Resolver una ecuación consiste en hallar los valores de la variable que hacen cierta la igualdad. Recuerda: Si un elemento está sumando en un miembro pasa al otro restando. Si está restando pasa sumado. Si un número multiplica a todos los elementos de un miembro pasa al otro dividiendo y si los divise pasa multiplicando.
ECUACIONES DE SEGUNDO GRADO
Una ecuación de segundo grado, ecuación cuadrática o resolvente es una ecuación poli nómica donde el mayor exponente es igual a dos. Normalmente, la expresión se refiere al caso en que sólo aparece una incógnita y que se expresa en la forma canónica:
donde a es el coeficiente cuadrático o de segundo grado y es siempre distinto de 0, b el coeficiente lineal o de primer grado y c es el término independiente.
Expresada del modo más general, una ecuación cuadrática en es de la forma:
con n un número natural y a distinto de cero. El caso particular de esta ecuación donde n = 2 se conoce como ecuación bicuadrática.
La ecuación cuadrática es de gran importancia en diversos campos, ya que junto con las ecuaciones lineales, permiten modelar un gran número de relaciones y leyes.
ECUACIONES DE TERCER GRADO
Una ecuación de tercer grado con una incógnita es una ecuación que se puede poner bajo la forma canónica:
ax³ + bx² + cx + d = 0,
donde a, b,c y d (a ≠ 0 ) son números que pertenecen a un cuerpo, usualmente. Sea K un cuerpo conmutativo, donde se pueden extraer raíces cuadradas y cúbicas. En este cuerpo, es posible factorizar por todo a ≠ 0, y la identidad siguiente es válida:
(a - b)3 = a3 - 3a2b +3ab2 - b3
Basta con encontrar una solución, digamos r, pues al factorizar ax3 + bx2 + cx + d por x - r, obtenemos una ecuación de segundo grado que sabemos resolver, lo que dará las demás raíces. En un cuerpo algebráicamente cerrado, se sabe que todo polinomio de grado 3 tiene tres raíces. Es el caso del cuerpo de los complejos, según el Teorema Fundamental del Álgebra.
Ficha técnica
Área:Matemáticas
Asignatura:Álgebra
Edad: No hay restriccion de edad
Herramientas:
Auto Aplicaciones
Bases de datos
Blogs
Códigos QR
Infografías

Crear proyectos de clase utilizando inteligencia artificial dando clic aquí
Tarea
SE REALIZARA UNA INVESTIGACION DE DONDE SE PUEDEN OBSERVAR LA APLICACION DE LAS ECUASCIONES DE PRIMER, SEGUNDO Y TERCER GRADO ADEMAS DE SU REPRESENTACION A TRAVES DE LA OBSERVACION DE OBJETOS MATEMATICOS.
EJEMPLO DEL OBJETO MATEMATICO:
EN UNA GRUA UNDUSTRAIL SE PUEDEN OBSEWRVAR LA APLICACION DE ECUASIONES YA QUE SE REQUIERE QUE LA GRUA ESTE EQUILIBRADA EN AMBAS PLUMAS:
COMO EJEMPLO:
UNA GRUA INDUSTRIAL CARGA MATERIAL CON UN PESO DE 20 TONELADA Y EN LA CONTRAPLUMA PARA EQULIBRARLA TIENE 4 HORMIGONES PARA EQUILIBRARLA. LA PREGUNTA ES CUANTO PESA CADA HORMIGON
SOLUCION 4X=20
X=20/4
X=5
CADA HORMIGON PESA 5 MTONELADAS PARA EQULIBRAR LA PLUMA.
DE ESTA MANERA USTEDES TENDRAN QUE INVESTIGAR DONDE Y EN QUE SE PLICAN LAS ECUACIONES
Procesos
ECUACIONES DE PRIMER GRADO
EJEMPLO
resolver la siguiente ecuación de primer grado 20x+10=50 paso
#1 agrupar termino semejantes
20x=50-10
paso # 2 se realizan las operaciones necesarias
20x=40
paso # 3 se despaja la incógnita "x" como coeficiente esta multiplicando a x al despajar pasa con la operación contraria x=40/20 por lo tanto el valor de x es : 2
ECUACIONES DE SEGUNDO GRADO
Para resolver ecuaciones de segundo grado utilizamos la siguiente fórmula:
omo vimos en la descripción, cualquier ecuación de segundo grado se puede expresar de la forma:ax2 +bx + c = 0
donde a, b y c serán números enteros (positivos o negativos). Para ello bastará obtener el denominador común (si hay denominadores), para eliminarlo y pasar todos los términos al primer miembro.
Sabemos que una vez conseguida dicha forma, las dos "posibles" soluciones de la ecuación son:
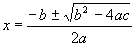
Así la ecuación del ejemplo inicial: 3x2 - 4x + 1 = 0: tendrá por soluciones: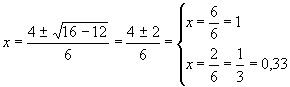
Luego 1 y 0,33 son las dos soluciones o raíces de la ecuación.
ECUACIONES DE TERCER GRADO
Los pasos de la resolución son:
- Dividir la ecuación inicial por el coeficiente a (a ≠ 0 ). Se obtiene:
x3 + b'x2 + c'x + d' = 0 con b' = b/a, c' = c/a, d' = d/a.
- Proceder al cambio de incógnita z = x + b'/3, para suprimir el término cuadrado. En efecto, al desarollar (z - b'/3)3 con la identidad precedente, vemos aparecer el término -b'z2, compensado exactamente por b'z2 que aparece en b'(z - b'/3)2. Se obtiene:
z3 + pz + q = 0, con p y q números del cuerpo.
- y ahora, la astucia genial: escribir z = u + v.
La ecuación precedente da (u + v)3 + p(u+v) + q = 0.
Desarollando: u3 + 3u2v + 3uv2 + v3 + pu + pv + q = 0.
Reagrupando: (u3 + v3 + q) + (3uv2 + v3 + pu + pv) = 0.
Factorizando: (u3 + v3 + q) + (u + v)(3uv + p) = 0.
Comó se ha introducido una variable adicional (u y v en vez de z) , es posible imponerse una condicion adicional. Concretamente:
3uv + p = 0, que implica u3 + v3 + q = 0 .
- Pongamos U = u3 y V = v3. Entonces tenemos U + V = - q y UV = - p3/27 porque UV = (uv)3 = (-p/3)3.
Por lo tanto U y V son las raíces de la ecuación auxiliar (E) X2 + qX - p3/27 = 0, que se sabe resolver.
Luego u y v son raíces cúbicas de U y V (que verifican uv = -p/3), z = u + v y finalmente x = z - b'/3. En el cuerpo C, si u0 y v0 son estas raíces cúbicas, entonces las otras son ju0 y j2u0, y por supuesto jv0 y j2v0, con j = e2iπ/3, una raíz cubica de la unidad.
Como el producto uv está fijado ( uv = -p/3) las parejas (u, v) posibles son ( u0, v0), ( ju0 , j2v0) y (j2u0, jv0).
Las otras raíces de la ecuación de tercer grado son por lo tanto ju0 + j2v0 - b'/3 y j2u0 + jv0 - b'/3.
Recursos
.videos
ver video
ecuaciones de primer grado
http://www.youtube.com/watch?v=wwlHv_9yajo&feature=related
ecuaciones de segundo grado
http://www.youtube.com/watch?v=n2ebqjrckjw&feature=rec-LGOUT-exp_fresh+div-1r-3-HM
ecuaciones de tercer grado
http://www.youtube.com/watch?v=Y1NoRAsb0Js
Evaluación
ECUACIONES DE PRIMER GRADOLa suma de las edades de A y B es 84 a˜nos, y B es 8 a˜nos menos que A. Hallar ambas
edades.
Soluci´on:
Sea x=edad de A.
Como B tiene 8 a˜nos menos que A; x-8=edad de B.
La suma de ambas edades es 84 a˜nos; luego tenemos la ecuaci´on:
Pague $87 por un libro, un traje y un sombrero. El sombrero cost´o $5 m´as que el libro
y $20 menos que el traje. ¿ Cu´anto pagu´e por cada art´Ä±culo?
Soluci´on:
No esta de m´as decir que la asignaci´on de la letra ”x”tiene mucho que ver en la simplicidad
de la resoluci´on del problema.
Sea x=precio del libro. Como el sombrero cost´o $5 m´as que el libro:
x + 5 = precio del sombrero
.
El sombrero cost´o $20 menos que el traje; luego, el traje cost´o $20 m´as que el sombrero;
x + 5 + 20 = x + 25 =
precio del traje.
Como todo cost´o $87; la suma de los precios del libro, del sombrero y el traje tiene
que ser igual a $87: de aqu´Ä± tenemos la ecuaci´on,
x + x + 5 + x + 25 = 87
Usando cualquier m´etodo para encontrar el valor buscado, tenemos que x=19, $19
precio del libro.
x+5=19+5=24, $24 precio del sombrero y
x+25=19+25=44, $44 precio del traje.
Checando el resultado con las condiciones iniciales; 19+24+44=87.
ECUACIONES DE SEGUNDO GRADO
EJERCICIOS
Utiliza la siguiente escena, cambiando los valores de los parámetros a, b y c de forma adecuada, para resolver las siguientes ecuaciones gráficamente.
a) x2 - 2x -1 = 0
b) x2 -1/4 = 0
c) 4x2 - 4x +1 = 0
PROBLEMAS DE APLICACIÓNLos siguientes problemas se plantean mediante una ecuación de segundo grado, aunque luego al resolverla pueda dar lugar a una ecuación de primer grado en algún caso.
Problema 1.- Calcular la hipotenusa de un triángulo rectángulo, sabiendo que las medidas de sus lados son tres números consecutivos
Solución: Se puede realizar el siguiente dibujo del problema, teniendo en cuenta que la hipotenusa el el lado mayor y llamando "x" al menor de los catetos.
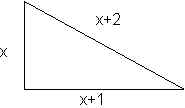
Teniendo en cuenta el teorema de Pitágoras, se cumple: (x+2)2 = (x+ 1)2 + x2.
Operando: x2 + 4x + 4 = x 2 + 2x + 1+ x2.
Agrupando todos los términos en el segundo miembro y simplificando: x2 - 2x - 3 = 0
Ecuación que sabes resolver numéricamente, con soluciones: x = 3 y x = -1 como puede verse en la siguiente escena.
Naturalmente la solución x =-1 hay que rechazarla porque un lado no puede tener una medida negativa, luego nos queda:
Hipotenusa: x + 2 = 5 ; Cateto mayor: x + 1 = 4 ; Cateto menor: x = 3.
Plantea la ecuación necesaria en cada caso para resolver los siguientes problemas. Resuélvelas numéricamente y también gráficamente usando la escena anterior
ECUACIONES DE TERCER GRADO
1) (x-1)^3 = x^3 - 3x^2 + 3x - 1
(2) (x+2)^3 = x^3 + 6x^2 + 12x + 8
(3) (x^3 - 1) = (x - 1) * (x^2 + x + 1)
(4) (x^3 + 8) = (x + 2) * (x^2 - 2x + 4)
(5) si x^3 + 4x^2 - 9x - 36 = 0
entonces x^2 * (x + 4) - 9 * (x + 4) = 0
entonces (x^2 - 9) * (x + 4) = 0
entonces (x - 3) * (x + 3) * (x + 4) = 0
Notas
.Creditos
Proyecto Creado Por Saul E. Cadena Benitez - Utilizando A Eduteka.org
*Nota: toda la información que aparece en los Proyectos de Clase y WebQuest del portal educativo Eduteka es creada por los usuarios del portal.
